椭圆切线方程公式推导
2025-04-27 08:05:09文/张鑫浩椭圆方程为x²/a²+y²/b²=1,对x求导可得：2x/a²+2yy'/b²=0,因此椭圆上任意一点(x,y)处的切线斜率k=y'=-b²x/(a²y)；若M(x₀,y₀)为椭圆上任意一点,则过M的切线方程为：y=[-b²x₀/(a²y₀)](x-x₀)+y₀。
椭圆切线方程公式的推导过程
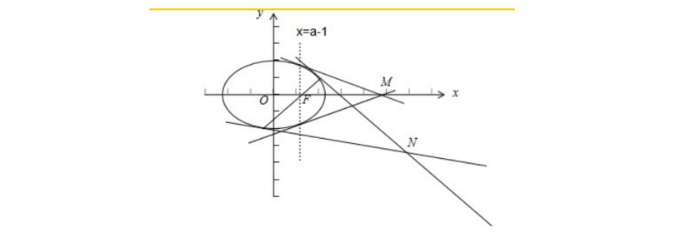
直线与椭圆的位置关系
直线与椭圆的位置关系分为三种：相离、相切、相交。
1.直线与椭圆相离的充要条件是直线与椭圆的方程组成的方程组无解,即所得一元二次方程的根的判别式小于0。
2.直线与椭圆相切的充要条件是直线与椭圆的方程组成的方程组有唯一解,即所得一元二次方程的根的判别式等于0。
3.直线与椭圆相交的充要条件是直线与椭圆的方程组成的方程组有两个不同的解,即所得一元二次方程的根的判别式大于0。
椭圆的第二定义 什么是椭圆椭圆是圆锥曲线的一种，即圆锥与平面的截线。下面小编...
2021-11-24
椭圆的面积公式是什么 怎么算的椭圆面积公式：S=π(圆周率)×a×b，其中a、b...
2021-10-29
椭圆的相关知识点 基本性质是什么椭圆是一种圆锥曲线。如果一个平面切截一个圆锥面，且...
2021-10-25
椭圆的第二定义 内容是什么平面上到定点F的距离与到定直线的距离之比为常数e(...
2021-10-25
椭圆的第三定义 内容是什么平面内的动点到两定点A1(a，0)、A2(-a，0...
2021-10-18
椭圆知识点椭圆（Ellipse）是平面内到定点F1、F2的距...
2020-12-15
椭圆长半轴和短半轴是什么椭圆截与两焦点连线重合的直线所得的弦为长轴，长为2...
2020-11-16
椭圆形的面积计算公式及例题椭圆面积公式：S=π(圆周率)×a×b，其中a、b...
2020-11-10
地球是椭圆的还是圆的地球是呈两极稍扁赤道略鼓的不规则的椭圆球体。地球（...
2020-11-09
椭圆的焦点坐标公式是什么椭圆的焦点坐标公式是高中数学常考的一个考点。下面小...
2020-10-19
高中椭圆的公式有哪些椭圆公式：（x-h）²/a²+（y-k）²/b²=...
2020-10-17
椭圆的标准方程是什么有很多同学想知道椭圆的标准方程是什么，下面小编为大...
2020-10-15
椭圆的相关知识点公式椭圆是平面内到定点F1、F2的距离之和等于常数（大...
2020-10-15
椭圆离心率公式及推导过程a²=b²+c²，c²=a²-b²，c=√(a²-...
2020-10-02
椭圆离心率公式c等于什么e=c/a=√[(a²-b²)/a²]=√[1-(...
2020-09-25
点击查看 中考资讯 更多内容
