2018江苏高考数学试题及答案解析【Word真题试卷】
2018-06-10 10:47:13文/李木子
温馨提示:全屏查看效果更佳。
绝密★启用前
2018年普通高等学校招生全国统一考试(江苏卷)
数学I
注意事项
考生在答题前请认真阅读本注意事项及各题答题要求
1. 本试卷共4页,包含非选择题(第1题 ~ 第20题,共20题).本卷满分为160分,考试时间为120分钟。考试结束后,请将本试卷和答题卡一并交回。
2. 答题前,请务必将自己的姓名、准考证号用0.5毫米黑色墨水的签字笔填写在试卷及答题卡的规定位置。
3.请认真核对监考员在答题上所粘贴的条形码上的姓名、准考证号与本人是否相符。
4.作答试题,必须用0.5毫米黑色墨水的签字笔在答题卡上的指定位置作答,在其他位置作答一律无效。
5.如需改动,须用2B铅笔绘、写清楚,线条、符号等须加黑、加粗
一、填空题:本大题共14小题,每题5小分,共计70分。请把答案填写在答题卡相应位置上。
2.若复数![]() 满足
满足![]() ,其中
,其中![]() 是虚数单位,则z
是虚数单位,则z![]() 的实部为__________.
的实部为__________.
3.已知5位裁判给某运动员打出的分数的茎叶图如图所示,那么这5位裁判打出的分数的平均数为__________.
![]()
4.一个算法的伪代码如图所示,执行此算法,最后输出的![]() 的值为__________.
的值为__________.

5.函数![]() 的定义域为__________.
的定义域为__________.
6.某兴趣小组有2名男生和3名女生,现从中任选2名学生去参加活动,则恰好选中2名女生的概率是__________.
7.已知函数![]() 的图像关于直线
的图像关于直线![]() 对称,则
对称,则![]() 的值是__________.
的值是__________.
8.在平面直角坐标系![]() 中,若双曲线
中,若双曲线![]() 的右焦点
的右焦点![]() 到一条渐近线的距离为
到一条渐近线的距离为![]() ,则其离心率的值是__________.
,则其离心率的值是__________.
9.函数![]() 满足
满足![]() ,且在区间
,且在区间![]() 上
上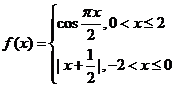 ,则
,则![]() 的值为__________.
的值为__________.
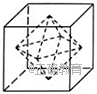
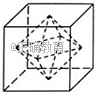
10.如图所示,正方体的棱长为2,以其所有面的中心为顶点的多面体的体积为__________.
11.若函数![]() 在
在![]() 内有且只有一个零点,则
内有且只有一个零点,则![]() 在
在![]() 上的最大值与最小值的和为__________.
上的最大值与最小值的和为__________.
12.在平面直角坐标系![]() 中,
中, ![]() 为直线
为直线![]() 上在第一象限内的点,
上在第一象限内的点, ![]() 以
以![]() 为直径的圆
为直径的圆![]() 与直线
与直线![]() 交于另一点
交于另一点![]() ,若
,若![]() ,则点
,则点![]() 的横坐标为__________.
的横坐标为__________.
13.在![]() 中,角
中,角![]() 所对应的边分别为
所对应的边分别为![]() 的平分线交
的平分线交![]() 于点
于点![]() ,且
,且![]() ,则
,则![]() 的最小值为__________.
的最小值为__________.
14.已知集合![]() ,将
,将![]() 的所有元素从小到大依次排列构成一个数列
的所有元素从小到大依次排列构成一个数列![]() ,记
,记![]() 为数列的前
为数列的前![]() 项和,则使得
项和,则使得![]() 成立的
成立的![]() 的最小值为__________.
的最小值为__________.
二、解答题
15.在平行四边形![]() 中,
中, ![]()
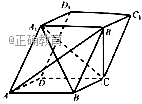
1.求证: ![]() 平面
平面![]()
2.平面![]() 平面
平面![]()
16.已知![]() 为锐角,
为锐角, ![]()
1.求![]() 的值。
的值。
2.求![]() 的值。
的值。
17.某农场有一块农田,如图所示,它的边界由圆![]() 的一段圆弧
的一段圆弧![]() 为此圆弧的中点
为此圆弧的中点![]() 和线段
和线段![]() 构成,已知圆
构成,已知圆![]() 的半径为
的半径为![]() 米,点
米,点![]() 到
到![]() 的距离为
的距离为![]() 米,先规划在此农田上修建两个温室大棚,大棚Ⅰ内的地块形状为矩形
米,先规划在此农田上修建两个温室大棚,大棚Ⅰ内的地块形状为矩形![]() .大棚Ⅱ内的地块形状为
.大棚Ⅱ内的地块形状为![]() ,要求
,要求![]() 均在线段
均在线段![]() 上,
上, ![]() 均在圆弧上,设
均在圆弧上,设![]() 与
与![]() 所成的角为
所成的角为![]()

1.用![]() 分别表示矩形
分别表示矩形![]() 和
和![]() 的面积,并确定
的面积,并确定![]() 的取值范围
的取值范围
2.若大棚Ⅰ内种植甲种蔬菜, 大棚Ⅱ内种植乙种蔬菜,且甲、乙两种蔬菜的单位面积年产值之比为![]() .求当
.求当![]() 为何值时,能使甲、乙两种蔬菜的年总产值最大.
为何值时,能使甲、乙两种蔬菜的年总产值最大.
18如图,在平面直角坐标系 ![]() 中,椭圆
中,椭圆![]() 过点
过点![]() ,焦点
,焦点![]() ,圆
,圆![]() 的直径为
的直径为![]()
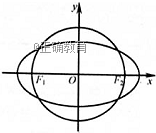
1.求椭圆![]() 及圆
及圆![]() 的方程;
的方程;
2. 设直线![]() 与圆
与圆![]() 相切于第一象限内的点
相切于第一象限内的点![]() .
.
①若直线![]() 与椭圆
与椭圆![]() 有且只有一个公共点,求点
有且只有一个公共点,求点![]() 的坐标;
的坐标;
②直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点.若
两点.若![]() 的面积为
的面积为![]() ,求直线
,求直线![]() 的方程.
的方程.
19记![]() 分别为函数
分别为函数![]() 的导函数.若存在
的导函数.若存在![]() ,满足
,满足![]() 且
且![]() ,则称
,则称![]() 为函数
为函数![]() 与
与![]() 的一个”
的一个”![]() 点”.
点”.
1.证明:函数![]() 与
与![]() 不存在”
不存在”![]() 点”.
点”.
2.若函数![]() 与
与![]() 存在”
存在”![]() 点”,求实数的值.
点”,求实数的值.
3.已知函数![]() ,对任意
,对任意![]() ,判断是否存在
,判断是否存在![]() ,使函数
,使函数![]() 与
与![]() 在区间
在区间![]() 内存在”
内存在”![]() 点”,并说明理由.
点”,并说明理由.
20设![]() 是首项为
是首项为![]() ,公差为
,公差为![]() 的等差数列,
的等差数列,![]() 是首项
是首项![]() ,公比为
,公比为![]() 的等比数列
的等比数列
1.设![]() ,若
,若![]() 对
对![]() 均成立,求
均成立,求![]() 的取值范围
的取值范围
2.若![]() 证明:存在
证明:存在![]() ,使得
,使得![]() 对
对![]() 均成立,并求
均成立,并求![]() 的取值范围(用
的取值范围(用![]() 表示)。
表示)。
参考答案
一、填空题
1.答案:![]()
解析:观察两个集合即可求解。
2.答案:2
解析:![]() ,故
,故![]()
3.答案:90
解析:![]()
4.答案:8
解析:代入程序前![]() 符合
符合![]() ,
,
第一次代入后![]() ,符合
,符合![]() ,继续代入;
,继续代入;
第二次代入后![]() ,符合
,符合![]() ,继续代入;
,继续代入;
第三次代入后![]() ,不符合
,不符合![]() ,输出结果
,输出结果![]() ,
,
故最后输出![]() 的值为
的值为![]() .
.

5.答案:![]()
解析:![]() ,解之得
,解之得![]() ,即
,即![]() .
.
6.答案:![]()
解析:假设![]() 名女生为
名女生为![]() ,男生为
,男生为![]() ,恰好选中
,恰好选中![]() 名女生的情况有:选
名女生的情况有:选![]() 和
和![]() ,
,![]() 和
和![]() ,
,![]() 和
和![]() 三种。
三种。
总情况有![]() 和
和![]() ,
,![]() 和
和![]() ,
,![]() 和
和![]() ,
,![]() 和
和![]() ,
,![]() 和
和![]() ,
,![]() 和
和![]() ,
,![]() 和
和![]() ,
,![]() 和
和![]() ,
,![]() 和
和![]() ,
,![]() 和
和![]() 这
这![]() 种,两者相比即为答案
种,两者相比即为答案![]()
7.答案:![]()
解析:函数的对称轴为![]()
![]() ,
,
故把![]() 代入得
代入得![]()
因为![]() ,所以
,所以![]() .
.
8.答案:2
解析:由题意画图可知,渐近线![]() 与坐标轴的夹角为
与坐标轴的夹角为![]() 。
。
故![]() ,故
,故![]() .
.
9.答案:![]()
解析:因为![]() ,函数的周期为
,函数的周期为![]() ,
,
所以![]()
∴![]() .
.
10.答案:![]()
解析:平面![]() 将多面体分成了两个以
将多面体分成了两个以![]() 为底面边长,高为
为底面边长,高为![]() 的正四棱锥,
的正四棱锥,
所以其体积为![]() .
.
11.答案:-3
解析:![]()
令![]()
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增
上单调递增
∵有唯一零点∴![]()
求导可知在![]() 上,
上, ![]()
∴![]()
12.答案:3
解析:∵![]() 为直径∴
为直径∴![]()
∴![]() 即
即![]() 到直线
到直线![]() 的距离。
的距离。
![]()
∵![]() ,又
,又![]()
∴![]()
设![]()
![]() 或
或![]() (舍去).
(舍去).
13.答案:9
解析:由面积得:![]()
化简得![]()
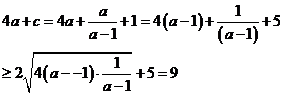
当且仅当![]() ,即
,即![]() 时取等号。
时取等号。
14.答案:27
解析:![]() 与
与![]() 相比,元素间隔大。所以从
相比,元素间隔大。所以从![]() 中加了几个
中加了几个![]() 中元素考虑。
中元素考虑。
![]() 个:
个: ![]()
![]() 个:
个: ![]()
![]() 个:
个: ![]()
![]() 个:
个: ![]()
![]() 个:
个: ![]()
![]() 个:
个: ![]()
发现![]() 时
时![]() 发生变号,以下用二分法查找:
发生变号,以下用二分法查找:
![]() ,所以所求
,所以所求![]() 应在
应在![]() 之间.
之间.
![]() ,所以所求
,所以所求![]() 应在
应在![]() 之间.
之间.
![]() ,所以所求
,所以所求![]() 应在
应在![]() 之间.
之间.
![]()
∵![]() ,而
,而![]() ,所以答案为
,所以答案为![]() .
.
二、解答题
15.答案:1.∵平行六面体![]()
∴面![]() 面
面![]()
∵![]() 面
面![]()
∴![]() 面
面![]()
又面![]() 面
面![]()
且![]() 面
面![]()
∴![]()
又![]() 面
面![]() 面
面![]()
∴![]() 面
面![]()
2.由![]() 可知:
可知: ![]()
∵![]()
∴![]()
∵平行六面体![]()
∴![]()
又由![]() 得
得![]()
∴四边形![]() 为平行四边形
为平行四边形
∵![]()
∴平行四边形![]() 为菱形
为菱形
∴![]()
又![]()
∴![]() 面
面![]()
∵![]() 面
面![]()
∴面![]() 面
面![]()
解析:
16.答案:1.方法一:
∵![]() ∴
∴![]()
又![]()
∴![]()
∴![]()
方法二:
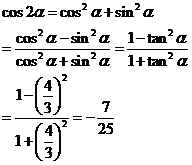
2.方法一:
![]() 为锐角
为锐角![]()
∵![]() 均为锐角,
均为锐角, ![]()
∴![]()
∴![]()
∴![]()
∴![]()
方法二:
∵![]() 为锐角
为锐角![]() ∴
∴![]()
∴![]()
∴![]()
∵![]() 为锐角∴
为锐角∴![]() 又∵
又∵![]()
∴![]()
∴![]()
∴![]()
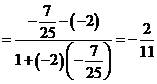
解析:
17.答案:1. 过![]() 作
作![]() 垂直于交圆弧
垂直于交圆弧![]() 于,设
于,设![]() 交
交![]() 于
于![]()
![]()
![]()
![]()
当![]() 点落在劣弧
点落在劣弧![]() 上时,
上时, ![]() ,与题意矛盾。
,与题意矛盾。
所以点![]() 只能落在劣弧上.
只能落在劣弧上.
所以![]() ,即
,即![]()
2.设甲种蔬菜年产值为![]() ,则乙种蔬菜年产值为
,则乙种蔬菜年产值为![]() ,设总年产值为
,设总年产值为![]()
则![]()
设![]()
令![]() ,解得
,解得![]() 或
或![]() ,根据
,根据![]() 舍去
舍去![]() ,记
,记![]()
|
|
|
|
|
|
|
|
| 单调递增 | 极大值 | 单调递减 |
| 单调递增 | 极大值 | 单调递减 |
答:当![]() 时,年总产值最大.
时,年总产值最大.
解析:
答案: 1.![]()
2.①![]() ②
②![]()
解析: 1.由题意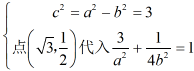
解得![]()
即椭圆标准方程为![]()
2.设![]() ,则
,则![]()
显然![]() 斜率存在,设
斜率存在,设![]() ,
,
则![]() ,
,![]()
将![]() 代入,得
代入,得![]()
∴![]() 与椭圆方程联立
与椭圆方程联立
得![]()
①与椭圆相切,则![]() ,即
,即![]()
将![]() 代入,解得
代入,解得![]() (舍去)或
(舍去)或![]()
由于![]() 在第一象限,则
在第一象限,则![]()
即![]()
②设![]() 与轴交点为
与轴交点为![]()
在![]() 中令
中令![]() ,得
,得![]() ,即
,即![]()
假设![]() 的纵坐标大于
的纵坐标大于![]() 的纵坐标
的纵坐标
![]()
而![]()
![]()
即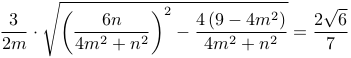
将![]() 代入
代入
化简得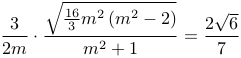
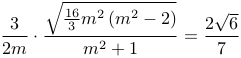
解此方程,得![]() ,(由已知条件,
,(由已知条件,![]() 舍)或
舍)或![]()
由于![]() 在第一象限,则
在第一象限,则![]()
回代入![]() ,得
,得![]()
答案: 1.![]()
若存在,则有![]()
根据![]() 得到
得到![]() 代入
代入![]() 不符合,因此不存在
不符合,因此不存在
2.![]()
根据题意有![]() 且有
且有![]()
根据![]() 得到
得到![]() 代入
代入![]() 得到
得到![]()
3.![]()
根据题意有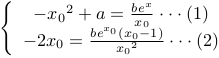
根据![]() 有
有![]()
转化为![]()
∵![]()
∴![]()
![]()
转化为![]() 存在零点
存在零点![]()
又![]()
∴恒存在零点大于![]() 小于
小于![]()
∴对任意均存在![]() ,使得存在"
,使得存在"![]() 点".
点".
答案: 1.由题意得![]() 对任意
对任意![]() 均成立
均成立
故当![]() 时
时
可得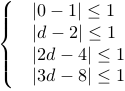 即
即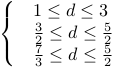
所以![]()
2.因为![]() 对
对![]() 均能成立
均能成立
把![]() 代入可得
代入可得![]()
化简后可得![]()
因为![]() ,所以
,所以![]()
而![]()
所以存在![]() ,使得
,使得![]() 对
对![]() 均成立
均成立
当![]() 时,
时,![]()
当![]() 时,设
时,设![]() ,则
,则![]()
设![]() ,因为
,因为![]() ,所以
,所以![]() 单调递增,又因为
单调递增,又因为![]()
所以![]()
设![]()
![]() ,且设
,且设![]() ,那么
,那么![]()
因为![]()
所以![]() 在
在![]() 上恒成立,即
上恒成立,即![]() 单调递增。
单调递增。
所以![]() 的最大值为
的最大值为![]() ,所以
,所以![]()
∴![]() 对
对![]() 均满足,所以
均满足,所以![]() 单调递减
单调递减
∴![]()
 江苏2021年体育类省统考考生健康应试须知 需要注意什么
江苏2021年体育类省统考考生健康应试须知 需要注意什么江苏省2021年普通高校招生体育类专业省统考将于4...
2021-03-24 江苏双一流大学名单
江苏双一流大学名单南京大学、东南大学、苏州大学、南京航空航天大学、南...
2021-03-10 江苏一高校为教职工提供托幼服务
江苏一高校为教职工提供托幼服务教职工的孩子送到幼托中心后,和母亲办公地方不到50...
2021-03-10 江苏对口单招本科考试形式
江苏对口单招本科考试形式专业技能考试+文化统考。专业技能考试形式和内容由各...
2021-03-09 江苏2021年高职院校提前招生网上申请时间
江苏2021年高职院校提前招生网上申请时间本文中,小编整理了江苏2021年高职院校提前招生相...
2021-03-09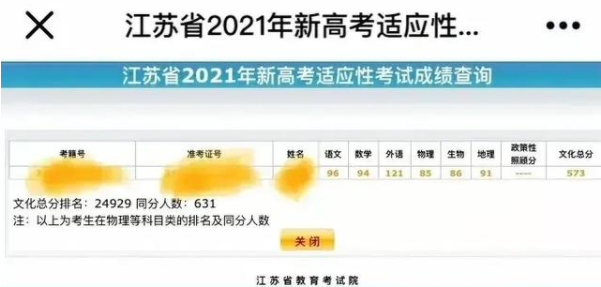 2021江苏八省联考成绩及一分一段表
2021江苏八省联考成绩及一分一段表目前,“八省联考”的成绩陆续公布。江苏已经出成绩了...
2021-03-09 江苏2021年新高考适应性考试成绩发布时间
江苏2021年新高考适应性考试成绩发布时间江苏2021年新高考适应性考试成绩发布时间已经公布...
2021-03-08 江苏明确教师不得用手机布置作业
江苏明确教师不得用手机布置作业江苏省教育厅近日下发《省教育厅办公室关于转发教育部...
2021-03-05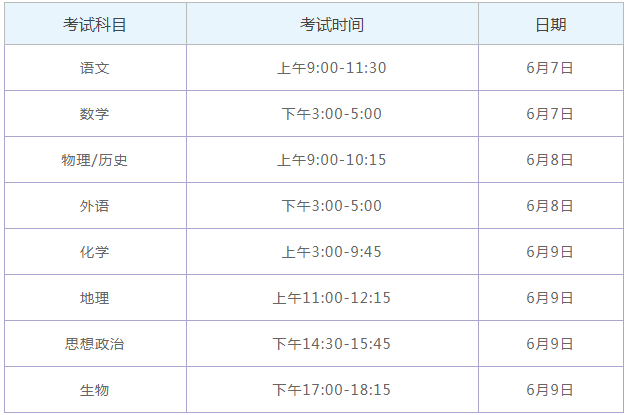 2021年江苏新高考考试时间安排及科目 什么时候高考
2021年江苏新高考考试时间安排及科目 什么时候高考2021年江苏新高考考试时间安排及科目已经确定,小...
2021-02-21 2021江苏八省联考成绩查询时间 什么时候出成绩
2021江苏八省联考成绩查询时间 什么时候出成绩2021江苏八省联考成绩查询时间是什么时候,跟随小...
2021-02-20 2021江苏高职单招报名时间及考试科目
2021江苏高职单招报名时间及考试科目小编整理了2021江苏高职单招报名时间及考试科目相...
2021-02-20 2021江苏高考多少分上二本 预计二本分数线
2021江苏高考多少分上二本 预计二本分数线2021江苏高考多少分上二本,预计二本分数线是多少...
2021-02-08 江苏2021年艺术类专业省统考成绩复核结果查询
江苏2021年艺术类专业省统考成绩复核结果查询江苏2021年艺术类专业省统考成绩复核已经结束,考...
2021-02-07 江苏省高考加分改革工作实施方案主要内容
江苏省高考加分改革工作实施方案主要内容为进一步促进高考公平,实现高考精准加分,江苏省教育...
2021-02-05 江苏2021年体育类专业招生考试科目
江苏2021年体育类专业招生考试科目江苏2021年普通高校体育类专业招生考试科目已经公...
2021-02-03
点击查看 江苏高考数学试题 更多内容